In laser processing, material undergoes intense phase changes from solid to liquid, and from liquid to vapor. In this section we focus on the discussion of liquid-vapor interface. This interface provides the important boundary conditions for laser machining modeling.

When the vapor pressure is equal to the ambient pressure (saturated condition), the gas-phase distribution function consists of a half-range Maxwellian with zero mean velocity for forward evaporated particles and the same for the back-scattered particles. The gas is in translational equilibrium. As the vapor pressure becomes larger than the ambient pressure, the distribution function for forward evaporated particles remains a half-range Maxwellian if the liquid is near thermodynamic equilibrium. But in the case of strong evaporation such as that in laser machining, there are relatively few back-scattered particles at the liquid-vapor interface. That is, the gas near the liquid-vapor interface is not in translational equilibrium when the evaporation is strong.

Here comes the name of Knudsen layer. In the case of strong evaporation such as in laser processing, the gas near the phase interface is not in translational equilibrium and the translational equilibrium is achieved within a few mean free paths by collisions between particles in a thin region, this region is called Knudsen layer region. The property across this layer is discontinuous. Many authors have contributed to the physics of this thin layer, Anisimov, Knight, Fink, Zweig, etc., to name a few. For details, the readers are referred to the papers in reference part. We sum up the conclusions here and try to avoid the complex physics which may be overwhelming to many people. Our purpose is to have a basic understanding of the Knudsen layer and can use the boundary conditions derived from it.

The theoretical model of the Knudsen layer is based on treating the region as a gasdynamic discontinuity across which certain jump conditions expressing conservation of mass, momentum and energy are applied. The particle properties across the Knudsen layer are discontinuous as shown below.

Figure 3.61 Property discontinuity across Knudsen layer

The following analytic relationships (Knight, 1979) are applied to account for the discontinuity of Knudsen layer.

,

,

,

,

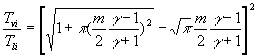where T , V, P and r are temperature, velocity, pressure and density respectively, subscript vi denotes the values of the vapor adjacent to the Knudsen layer and li the values of liquid adjacent to the Knudsen layer. Ma_v is the vapor Mach number_, and erfc(m) the complementary error function.

The gas velocity is obtained from mass conservation:

where v_i is the velocity of melt-vapor interface and v_v is the vapor velocity.

The liquid-vapor boundary condition in laser machining is very complex. It is the balance of energy basically, but the energy involved includes incident laser energy, heat transfer (conduction heat loss, convection and radiation heat loss), energy change through phase changes, and the energy carried away by the mass flow caused by the strong vaporization.

At the melt-vapor front, the Stefan boundary condition is applied,

,

,

where Q is the laser heat flux which depends on reflectivity Rl, absorptivity b and the plasma correction coefficient C. I is the laser intensity which is a function of time, and b is the laser beam radius. Q_th is the energy from heat transfer. The subscripts l, v and i denote liquid phase, vapor phase and vapor-liquid interface, respectively. The gas energy E_v includes the internal energy and the kinetic energy. k is the heat conductivity, v the velocity, R the universal gas constant, g the specific heat ratio, L_v the latent heat of vaporization, and M_v the molecular mass. The velocity, the laser energy flux and the heat conduction flux are valued along the normal direction of the target geometry. The vapor-liquid front is determined by tracing the temperature. As long as the temperature at certain grid points reach vaporization temperature, the grids which have temperatures larger than vaporization temperature are taken out as the gas phase and the calculation starts from the newly determined vapor-liquid front.

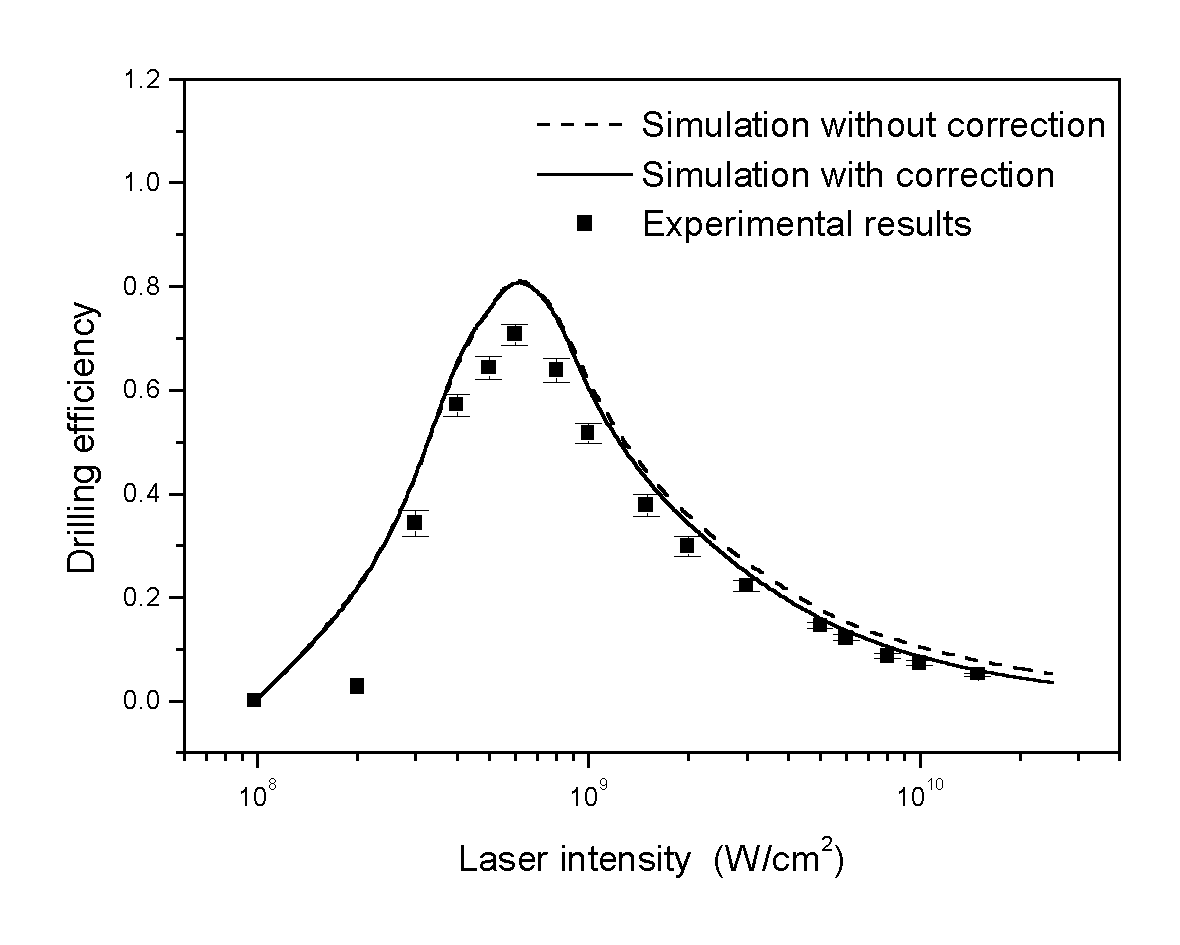
Using the enthalpy method to deal with the phase change problem, using the above mentioned boundary conditions, a 2D axisymmetric model was built to simulate the drilling process of copper using frequency tripled Nd:YAG laser. Laser wavelength is 355 nm, pulse duration is 50 ns, pulse repetition rate is 2KHz. Different energy levels are used to explore the optimum conditions for UV laser drilling of pure copper. Figure 3.60 shows SEM pictures of holes drilled at different energy levels. Figure 3.61 shows how the depth of hole and drilling efficiency vary with laser intensity. Figure 3.62 shows how the diameter of holes vary with laser intensity. For details, please refer to the original paper of Zhang, 2000.

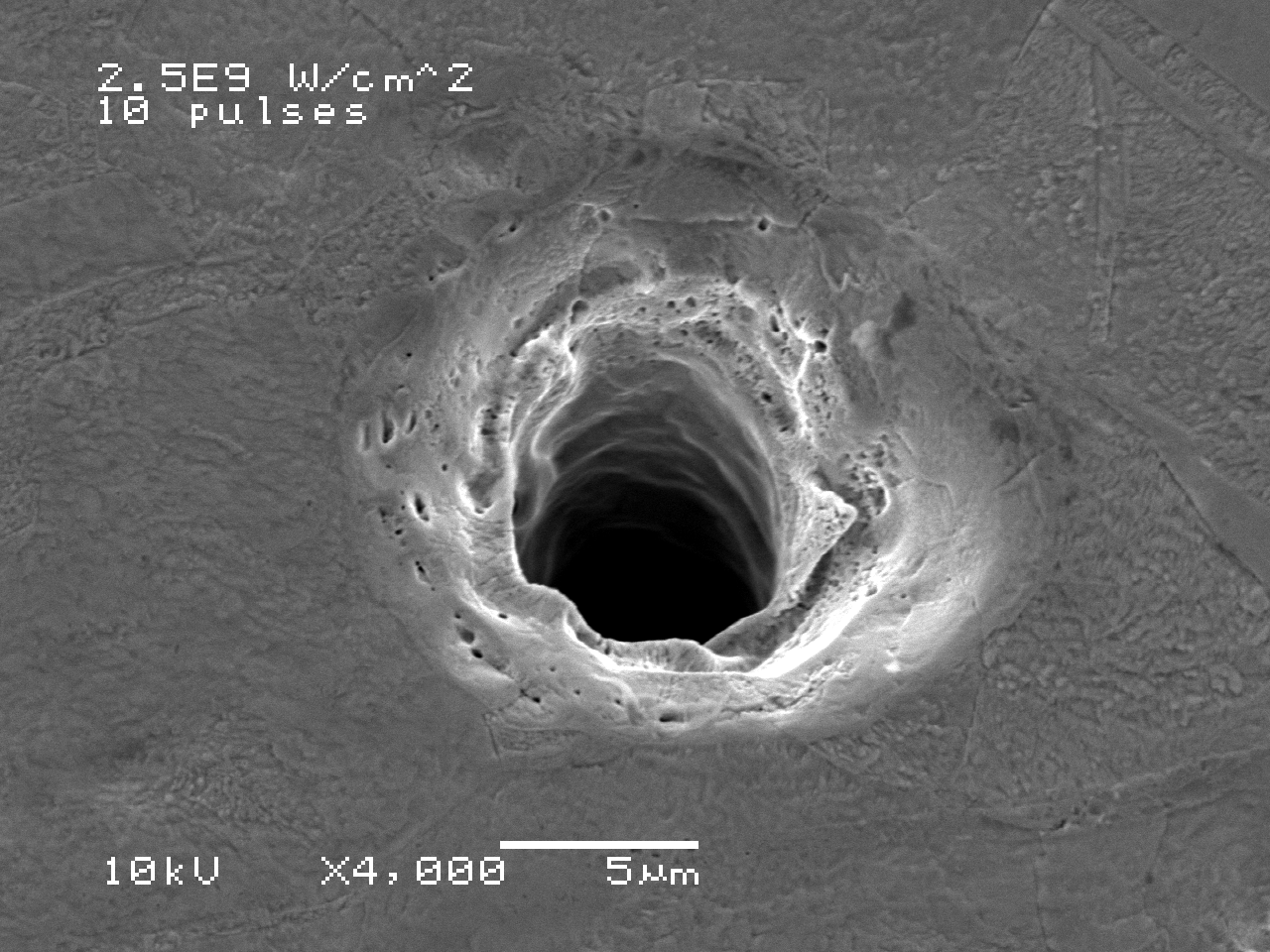
Fig. 3.62 SEM micrographs of laser drilled holes, upper figure: I = 2.5´ 10⁹ W/cm², 10 pulses; and Lower figure: I = 2.5´ 10⁹ W/cm², 50 pulses (Wavelength l = 355 nm, Gaussian beam, beam radius b = 2.25 m m, pulse duration 50 ns, repetition rate 2 KHz, Cu)

(a)

Fig. 3.63 (a) Drilling depth per pulse; and (b) Drilling efficiency (Wavelength l = 355 nm, Gaussian beam, beam radius b = 2.25 m m, pulse duration 50 ns, Cu)

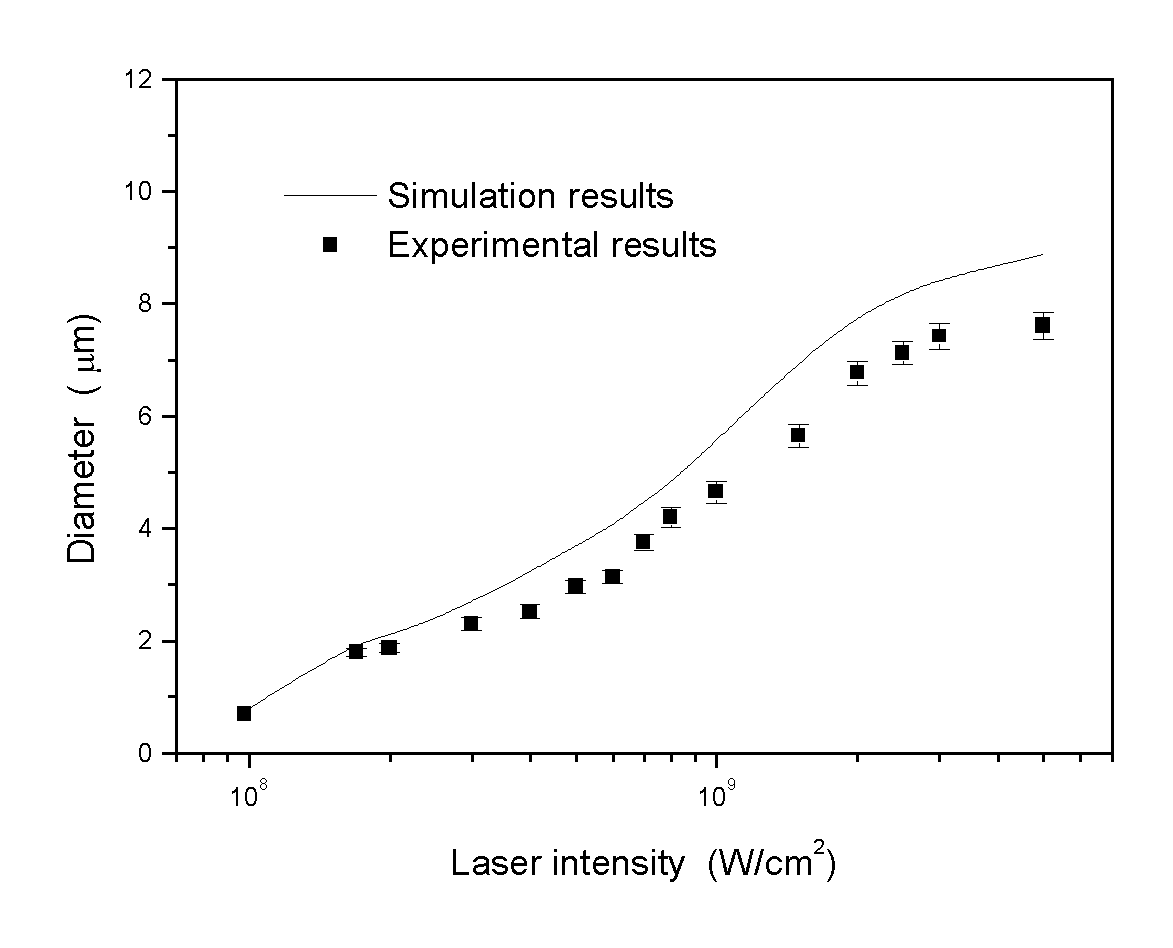
Fig. 3.64 Single pulse drilled hole diameters vs. laser intensity (Wavelength l = 355 nm, Gaussian beam, beam radius b = 2.25 m m, pulse duration 50 ns, Cu)

References:

Anisimov S. I. et al., 1971, Effects of High-power Radiation on Metals

Knudsen M., 1909 Ann. Phys., Lpz. 28 999

Finke B. R. and G. Simon, 1988, "On the gas kinetics of laser-induced evaporation of metals," J. Phys. D: Appl. Phys. 23 (1990) 67-74.

Knight, C. J., "Theoretical Modeling of Rapid Surface Vaporization with Back Pressure," AIAA Journal, Vol. 17., No. 5, May 1979.

Wenwu Zhang, Y. Lawrence Yao,"Modeling and Analysis of UV Laser Micro-machining of Copper," ICALEO 2000.

Congradualations! You have reached the end of chapter 3, level three. Hoping our efforts bring you some thing. Please do the following chapter quiz, then move on to next chapter.

Level 3 Chapter 3 Quiz