S3.4 Modeling of Laser Machining Process (1)
Laser machining is a thermal process which removes material through phase changes (melting, vaporization). Before we introduce the readers to the models used in LMP, it is necessary to have a brief review of the related thermal processes. These include conduction, convection and radiation heat transfer. Knowledge of Fluid mechanics is also needed in reading the literatures of LMP. We will also talk about the energy involved in state changes of materials.
Review of heat transfer:
Heat transfer is energy in transit due to temperature differnece. Conduction, convection and radiation are the three basic heat transfer mechanisms.
Conduction Heat Transfer:
Conduction is the transfer of energy from a more energetic to the less energetic particles of substances due to interactions between the particles. In gas and liquids, heat conduction takes place through random molecular motions (difusions), in solid heat conduction is through lattice waves induced by atomic motions. In nonconductor, the energy transfer is exclusively through such lattice waves, in conductors, the motion of free electrons also contribute to heat conduction.
Fourier Law is the rate equation based on experimental evidences. This law states that heat flux at the surface normal is proportional to the temperature gradient.
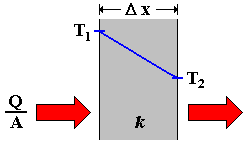
Figure 3.16: 1D heat transfer
For 1D heat conduction in x-direction:
q"=-k dT/dx
Where k is thermal conductivity (W/m.K), T is temperature (K), q" is the heat flux in x direction.
General form of Fourier's Law is:
q" = - k Ñ T(x,y,z,t) = -k(i¶ T/¶ x + j¶ T/¶ y + k¶ T/¶ z)
Thermal conductivity k is a material property, it may vary with temperature and pressure. In laser machining which usually involves solids, the dependence on temperature should be considered. This makes k a function of temperature k(T), such function relations are found through interpolation of experimental results at various temperatures.
Using energy balance relations, ie., increase of stored energy in a volume of material = energy in + energy generation in this volume - energy out, we can deduce the general differential form of three dimensional heat conduction equation. In short:
Ein + Eg - Eout = D Est
General equation of Heat Conduction:
¶ (k¶ T/¶ x)/¶ x +¶ (k¶ T/¶ y)/¶ y +¶ (k¶ T/¶ z)/¶ z + dq/dt =r cp (¶ T/¶ t)
T= T(x,y,z,t). Steady state: (¶ T/¶ t)=0
If material is of constant property, we can pull k out and we get:
¶ 2T/¶ x2 + ¶ 2T/¶ y2 + ¶ 2T/¶ z2 + (dq/dt)/k = (r cp/k) (¶ T/¶ t) =1/a (¶ T/¶ t)
a = k/(r cp) is the thermal difusivity.
In cylindrical coordinates we have:
Fourier Law: q" = - k Ñ T(r,f ,z,t) = -k(i¶ T/¶ r + j(1/r)¶ T/¶ f + k¶ T/¶ z)
General equation of Heat Conduction:
(1/r)¶ (k¶ T/¶ r)/¶ r +(1/r2)¶ (k¶ T/¶ f )/¶ f +¶ (k¶ T/¶ z)/¶ z + dq/dt =r cp (¶ T/¶ t)
Where r is the radial direction, f is the circumferential direction, z is the axial direction.
When we assume axissymetric heat transfer, which happens frequently in laser drilling modeling, we mean that the variation of temperature in the f direction is zero. Then the above equation becomes:
(1/r)¶ (k¶ T/¶ r)/¶ r +¶ (k¶ T/¶ z)/¶ z + dq/dt =r cp (¶ T/¶ t)
Similarly in spherical coordinates:
q" = - k Ñ T(r,q ,f ,t) = -k(i¶ T/¶ r + j(1/r)¶ T/¶ q + k(1/r sinq )¶ T/¶ f )
(1/r2) ¶ (kr2¶ T/¶ r)/¶ r + (1/r2sin2 q ) ¶ (k¶ T/¶ f )/¶ f + (1/r2 sinq ) ¶ (k sinq ¶ T/¶ q )/¶ q + dq/dt =r cp (¶ T/¶ t)
These equations are complex, but they still state the conservation of energy.
Convection Heat Transfer:
Convection usually refers to the energy transfer between a solid surface and an adjacent moving gas or liquid. Convection heat transfer is a combination of diffusion or molecular motion within the fluid and the bulk or macroscopic motion of the fluid.
The rate of energy transfer from a system to the fluid is quantified by Newton's law of cooling:
q" = h(Tfluid - Ts)
where q" is the convective heat flux (W/m2), h is the convective heat transfer coefficient (W/m2K), Ts is the surface temperature (K) and
Tfluid is fluid temperature away from the surface (K).
The heat transfer coefficient, h, is an empirical parameter that encompasses the effects of the fluid flow near the surface, the fluid properties, and the surface geometry. The decision of h is the most important task in convection heat transfer analysis. Many emperical formulations are put forward, readers should refer to textbook of Heat Trasfer for detailed information. Convective heat transfer is coupled with the fluid dynamics of the system. The following figure show the boundary layer development of a uniform flow along a flat plate.
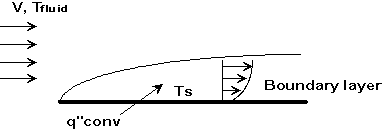
Figure 3.17: illustration of Boundary layer and convection heat transfer
Radiation Heat transfer:
Unlike conduction and convection, radiation does not require the presence of a medium to propagate. Actually, radiation transfers heat energy most efficiently in a vacuum. Radiation energy is transported by electromagnetic waves. Thermal radiation is energy emitted by matter at a finite temperature as a result of changes in the electron configurations of the atoms or molecules. Generally, radiation heat transfer analysis is focused on solid surfaces but emission may also occur from liquids and gases.
Stefan-Boltzmann Law states that emissive power E of a surface is proportional to T4 :
E=e s Ts4,
Where e is surface emissivity; s =5.67*10-8W/m2.K4 is the Boltzmann constant.
The energy absorbed by the surface is:
Gabs=a G=a s Tsur4,
where a is absorptivity; G is the irradiation from the surroundings.
So the net heat transfer of radiation energy from a finite surface to the infinite surrouding is:
q"rad=E- Gabs=e s Ts4-a s Tsur4
Where Ts and Tsur are the surface and surrounding temperatures.
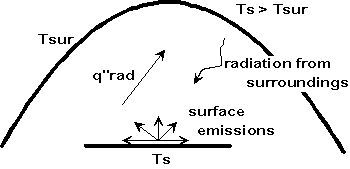
Figure 3.18: radiation energy exchange between a surface and the surounding
The real analysis of radiation energy exchange is far more complex than what we see here. Radiation relates to direction, area, wavelength, surface condition, etc. We also see that radiation increases with 4th power of temperature, thus at high temperature the radiation heat transfer should be considered.
Review of Fluid Mechanics:
Detailed discussion of convective heat transfer is based on Fluid Mechanics. So it is necessary to give a brief review of some basic concepts and relations in fluid mechanics. These include:
1. Eulerian and Lagrangian Descriptions:
There are two basic coordinate systems which may be used in mechanics. In Eulerian framework the independent variables are the spatial coordianates x,y,z and time t. Attention is focused on the fluid that passes through a control volume which is fixed in space, the fluid inside the control volume at any instant in time will consist of different fluid particles from that which was there at some previous instan in time. In Lagrangian approach, attention is focused on a particular mass of fluid as it flows, in this frame, x,y,z,t are no longer independent variables, the independent varialbles are x0, y0, z0 at time t0 and time t. All positions of the mass we are considering can be calculated if the velocity field is known.
Let F be any field variable such as density or temperature, F=F(x,y,z,t) in Eulerian description or F= F(x0,y0,z0,t) in Lagrangian description. Then, the time derivative of F is DF/Dt, and we have:
![]() ,
where u, v, w are velocities in the x, y, z directions.
,
where u, v, w are velocities in the x, y, z directions.
2. Conservation of mass
Consider a specific mass of fluid whose volume V is arbitrarily chosen. This fluid mass is followed as it flows, its shape and size can change with time, but its mass will remain unchanged unless some mass generation/extinction mechanism exists (nuclear reaction for example). So the conservation of mass states that the Lagrangian derivative of the mass of the fluid inside the volume is zero. In mathematical form:
![]() (Integration
form)
(Integration
form)
The PDE form of conservation of mass is:
![]() where
xk and uk are coordinates and velocity in the k=1,2,3
directions.
where
xk and uk are coordinates and velocity in the k=1,2,3
directions.
If the fluid is incompressible, then we have:
![]()
Combine this relation with the general law of mass conservation, we have the well known Continuity Equation for incompressible flows:
![]()
3. Conservation of Momentum
The principle of conservation of momentum is an application of Newton's second
law of motion to an element of the fluid. Considering a given mass of fluid
in a Lagrangian frame, this law states that the rate at which the momentum of
the fluid mass is changing is equal to the net external force acting on the
mass. The external forces may be classified as body forces (such as gravitational
or electromagnetic forces) ![]() and
surface forces (such as pressure forces or viscous forces)
and
surface forces (such as pressure forces or viscous forces) ![]() .
Thus we have:
.
Thus we have:
![]()
After many manipulations, using continuity relation and Renolds' Transport
Theorem, and relate the surface force to the stress tensor ![]() and
surface normal ni, (i=1,2,3 , j=1,2,3). We got the Momentum equations:
and
surface normal ni, (i=1,2,3 , j=1,2,3). We got the Momentum equations:
![]()
![]()
Here we used summation convention. The above equation is in fact three equations. We don't have space to explain all the derivation details and the summation conventions. It's important to understand the physical meanings of these equations.
The constitutive relations relate the stress tensor with the pressure and fluid velocity field by introducing some material coefficients. Assuming Newtonian fluid, we have:
![]() ,
where p is pressure, m
is dynamic viscocity, l
is another material coefficient.
,
where p is pressure, m
is dynamic viscocity, l
is another material coefficient.
Taking this relation into the Equation of momentum conservation, we derive the famous Navier-Stokes Equation:
![]()
Again this equation uses summation convention and represent three scalar equations.
Under the condition of incompressible flow and the dynamic viscosity to be constant, the Navier-Stokes equation becomes:
![]()
When viscous is neglected, we have the Euler equations:
![]()
4. Conservation of Energy
Apply the first law of thermodynamics to fluid element, we have the principle
of conservation of energy in fluid mechanics. Consider any arbitrary mass of
fluid of volume V and follow it in a lagrangian frame of reference as it flows.
The total energy of this mass per unit volume is the combination of internal
energy and kinetic energy, ![]() .
The rate of change of the energy of the mass we are following is balanced by
the works done by external forces minus the energy the mass give to the outside.
In integral form, this relation is:
.
The rate of change of the energy of the mass we are following is balanced by
the works done by external forces minus the energy the mass give to the outside.
In integral form, this relation is:
![]()
Applying the relation of continuity and momentum, we get the equation of conservation of thermal energy:
![]()
This equation is the balance of thermal energy only, it comes from the subtraction of mechanical energy from the original energy balance relation. But it is usually refereed to as the Energy Equation.
Taking stress relation into the above equation, we have:
![]()
where T is temperature, k is the thermal conductivity, ![]() is
the dissipation function defined as:
is
the dissipation function defined as:
![]()
For incompressible fluid in cartesian frame, ![]() .
.
5. State equations of materials
Two state equations are needed to make the above relations self-contained.
![]()
We know for perfect gas P=r RT, and internal energy e=CvT, with Cv be the constant volume specific heat.
Some times enthalpy is used in the energy equation, enthalpy is defined as:
![]()
From discussion of 2, 3, 4 and 5, we have shown seven scalar equations with 7 variables (assume k, l and m are known). For most general case, these relations are coupled. But usually we can simplify them, either for 1D or 2D flow, or we assume some specific conditions. Assume incompressible flow or neglecting viscous can simplify the equation. If we neglect the velocity in the energy equation, we can get the heat conduction equation. Assume irrotational flow results in the analysis of potential flow.
The model may becomes more complex when turbulence is considered. Turbulence surely takes effect in actual applications, but we don't have time to cover it here. Another complexity comes from shock-wave which is common for high energy laser machining. We will see some discussions in following sections.
Are you bored of these mess of math? I guess you need to figure them out in order to read the literatures in this area. I can not take the task of fluid mechanics, if you could not understand the meaning of these relations, you are suggested to turn for a book on Fluid Mechanics. If you feel comfortable for this section, then you will feel comfortable for the following sections.
Boundary layers and potential flows are discussed extensively in fluid mechanics. Let's show you some pictures in addition to the boring equations.
The flow pattern of a dipole
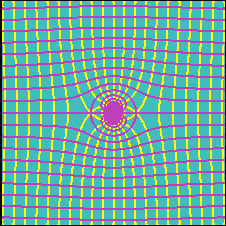
Flow around a cylinder

Flow around a airfoil
Figure 3.19 Some patterns of fluid field (Courtesy of UNIVERSITY OF GENOA, HYDRAULIC INSTITUTE)